E类射频放大器设计用于产生具有特定特性的开关波形。在本文中，我们讨论了这些波形的优点和局限性。
本文引用地址：
从某种意义上说，功率放大器设计是一门理解和整形波形的艺术，以实现高效率，同时满足其他规范的可接受水平，如输出功率、线性度和功率增益。例如，E类功率放大器通过使用专门设计的负载网络来塑造开关电压和电流波形，以实现效率最大化。
我们在上一篇文章末尾首次看到的图1显示了E类放大器的典型开关波形。电压和电流的转变在时间上彼此错开，导致波形不重叠。
E类放大器中的典型开关电流和电压波形。
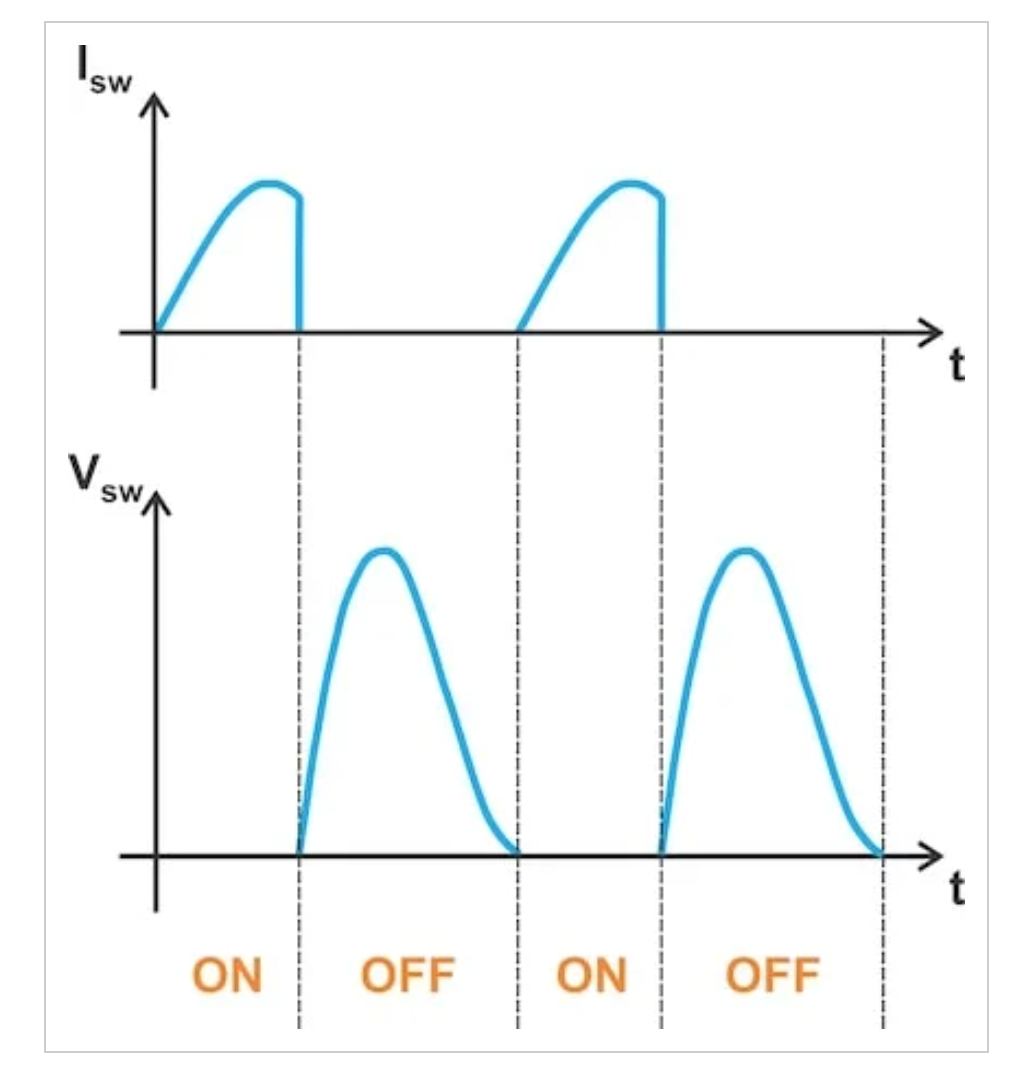图1.E类射频功率放大器中的典型开关电流（顶部）和电压（底部）波形。图片由Steve Arar提供请注意，上述波形是典型的，并不理想。在本文中，我们将探讨E类放大器最佳波形的特性，如图2所示。在深入研究了这些波形的可取之处之后，我们将讨论一个重要的限制，这个限制使得它们几乎无法实现。
E类射频功率放大器的目标电流和电压波形。
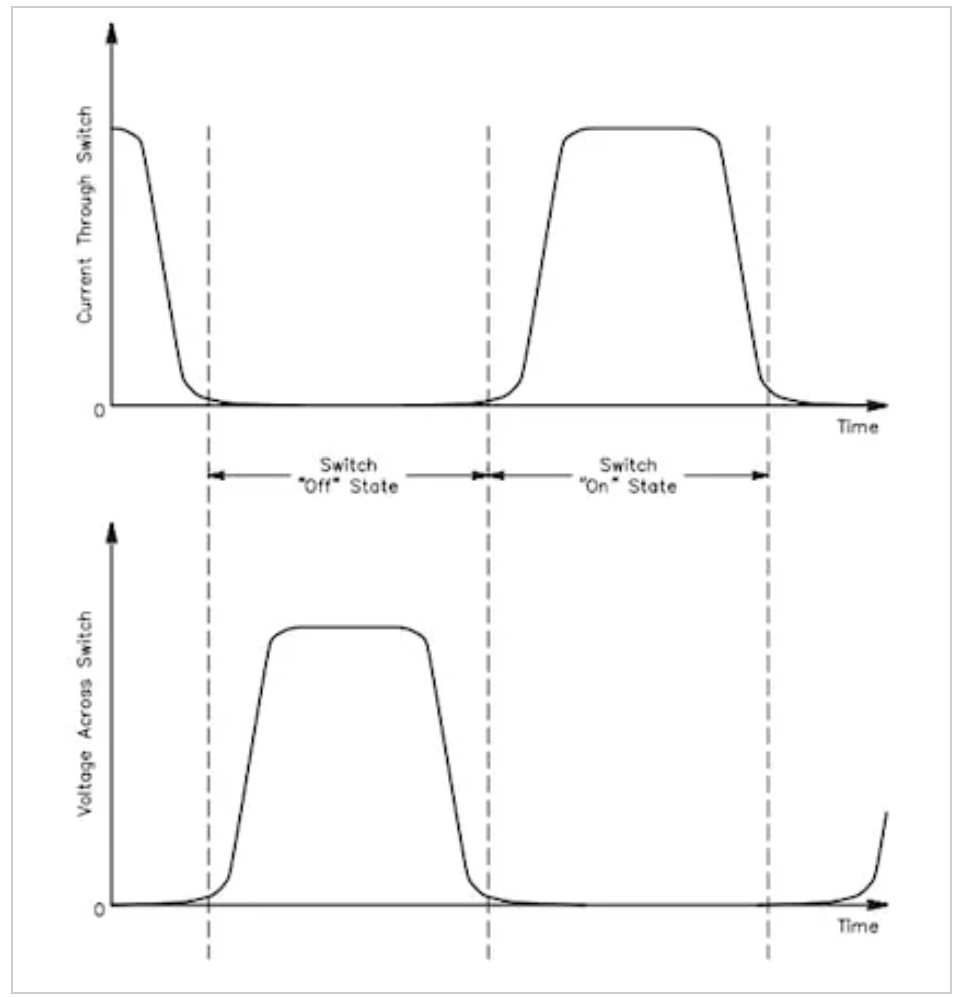图2:E类射频功率放大器的目标电流（顶部）和电压（底部）波形。图片由Nathan O.Sokal提供让我们从检查这些波形如何在OFF到ON和ON到OFF转换期间防止功率损失开始。
目标波形的重要特征
在这些波形中，在开关接通之前，开关两端的电压降至零（Vsw=0）。在开关接通的那一刻，电压的斜率为零（dVsw/dt=0）。同样，在设备关闭之前，通过开关的电流降至零（Isw=0）。在关闭时刻，我们有Isw=0和dIsw/dt=0。
消除开启转换期间的电源损失
寄生电容不可避免地会与实际开关并联出现。由于电压降至Vsw=0，当开关接通时，这些电容不充电。这有效地消除了因放电这些电容而导致的功率损失。
零斜率的重要性可能并不那么明显。然而，条件Vsw=0和dVsw/dt=0意味着Vsw在开关接通时刻之前保持在0V一段时间，从而确保了开关可以接通而不会造成功率损失的间隔。因此，放大器的轻微失谐不会显著降低效率。对于那些有兴趣并可以访问IEEE数据库的人来说，Nathan O.Sokal和Alan D.Sokal在“E类——一类新型高效调谐单端开关功率放大器”中更详细地介绍了零斜率条件的重要性。
同样值得注意的是，一旦开关打开，E类放大器中的开关电流就会从零平稳上升。由于实际晶体管的dI/dt能力有限，因此开关电流从零上升会缩短过渡时间。
最后，当晶体管从截止状态切换到完全导通状态时，其电导从零逐渐增加。另一种思考方式是，开关电阻（R）在完全接通时减小。由于电阻在电流逐渐增加的同时逐渐减小，I2R功率损耗最小化。
当开关的开启转换缓慢时，这尤其有用。我们可以预期，满足Vsw=0和dVsw/dt=0条件的E类放大器即使在开启过渡时间包含高达30%的RF周期时，也会有较小的I2R功率损耗。
消除关闭转换期间的电源损失
我们上面提到过，在设备关闭之前，通过开关的电流降至零（Isw=0）。这可以防止与开关串联出现的不可避免的寄生电感发生突然的电流变化。电流波形的这种跳跃将导致关断转换期间的功率损失，我们稍后将对此进行讨论。
开关断开时刻的条件Isw=0和dIsw/dt=0意味着Isw在该时刻之前的一段时间内达到0A。与OFF到ON转换期间的电压条件一样，这降低了放大器轻微失谐降低效率的程度。
实现目标波形的局限性
Bela Molnar的论文“单端开关模式调谐（E类）功率放大器可实现波形的基本限制”证明，图2中的目标波形在实际的E类放大器中无法实现。Molnar表明，如果电路要向负载提供非零输出功率，则不可能在开关的关断和接通转换时都有零电压和零电流。
为了具有非零输出功率，我们需要电压和/或电流波形中的跳跃不连续性。这就是为什么图1中提供的典型E类波形（其中在开关时刻Vsw=0）在开关关闭时显示电流的跳跃不连续性。让我们来看看这是如何导致功率损失的。
关断过渡过程中非零电流的影响
在继续之前，请注意本节包含大量的理论数学。关键的结论是，如果开关串联有电感，则开关关断时刻的非零开关电流会导致功率损失。如果你对这背后的微积分感兴趣，请继续阅读——否则，你可能想跳到本节的末尾。
至此，让我们继续考虑图3中的简化开关模式放大器。在这个电路图中，L2是与开关串联出现的工作频率下的有效电感。L1近似于RF处的开路。
电感L2与开关串联的简化开关模式功率放大器的电路图。
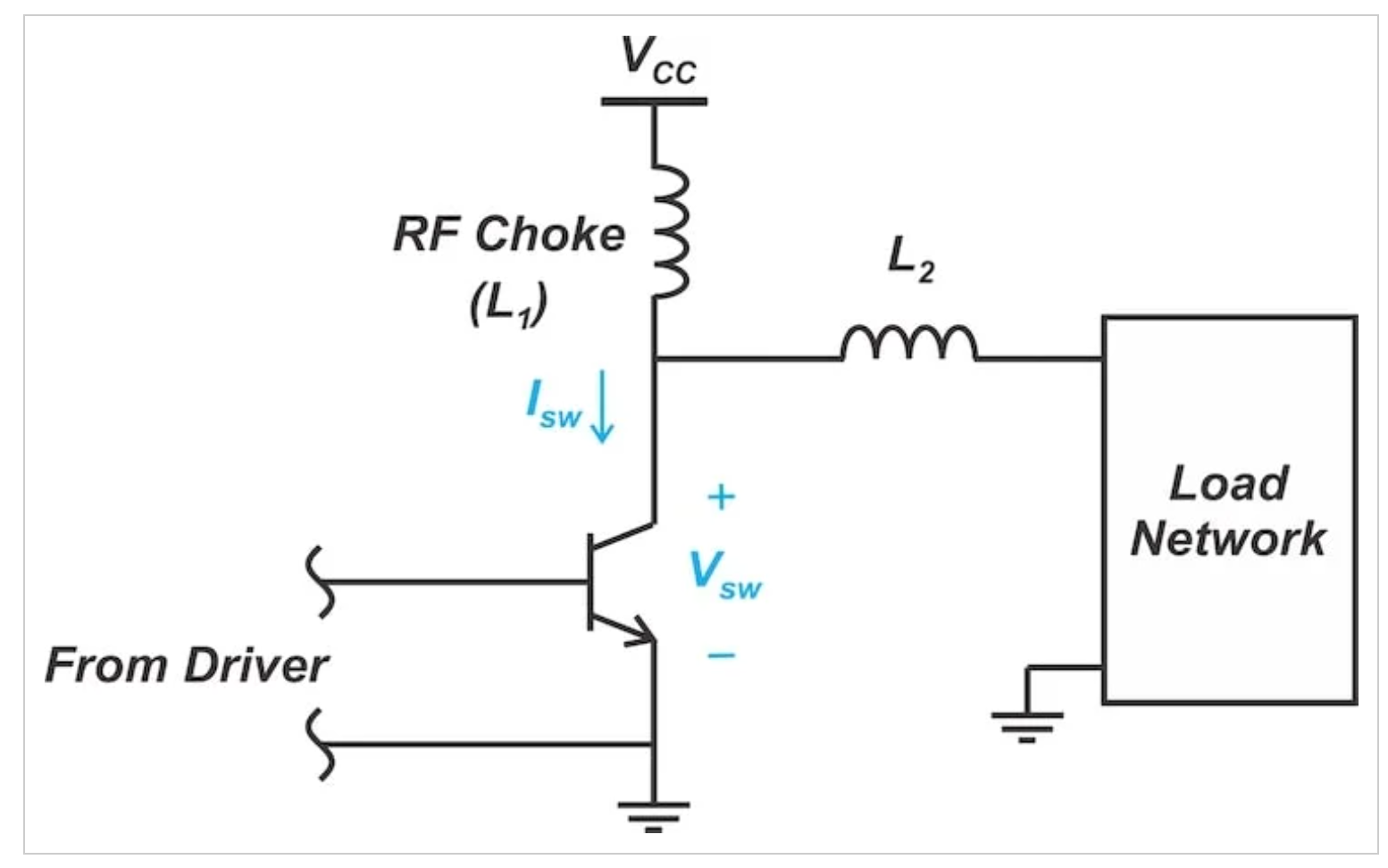图3.一种简化的开关模式功率放大器，电感L2与开关串联。图片由Steve Arar提供假设图3中的开关在t=t0时关闭。此时的开关电流和电压波形如图4所示。
通过开关的电流波形和开关两端的电压波形。
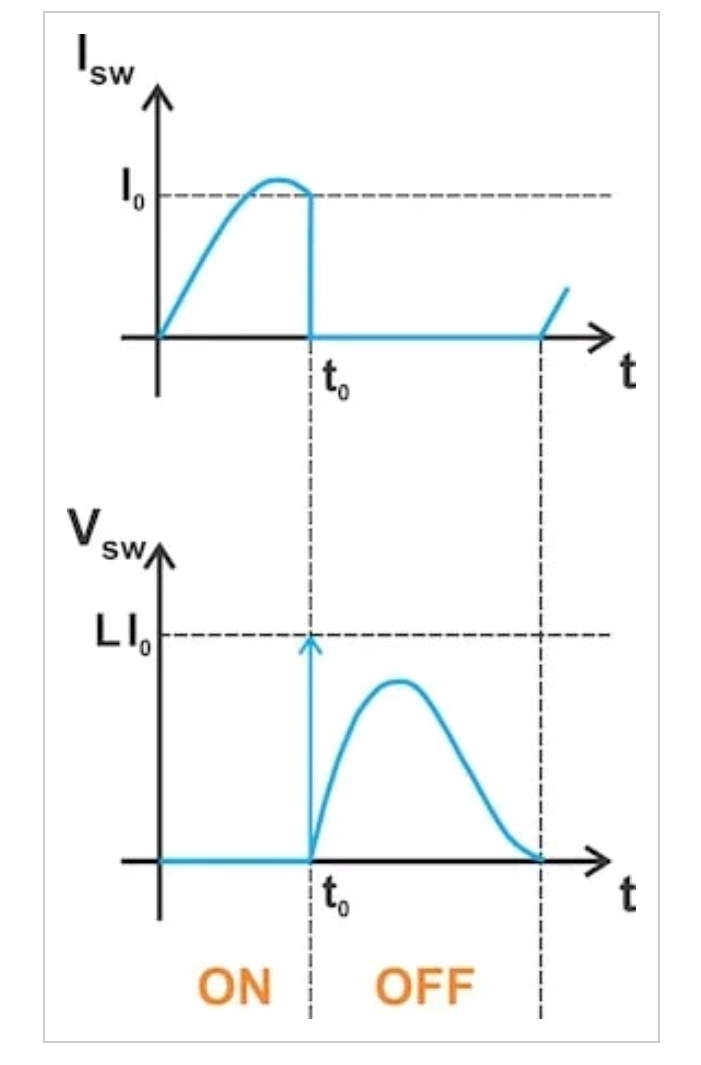图4.通过开关的电流（顶部）和开关两端的电压（底部）。图片由Steve Arar提供在上图中，通过电感器的电流在t0之前具有非零值I0。在t=t0时，电流仍为I0；t0+之后，它为零。电感器中的电流不能瞬间改变，除非电路中施加或支持脉冲电压——狄拉克δ函数（t）。这可以通过注意到单位冲激函数δ（t）随时间的积分是单位阶跃函数（波形中的跳跃）来理解。
换句话说，对具有跳跃不连续性的波形进行微分会导致导数波形内的脉冲函数。由于电感器两端的电压（v）与其电流的导数成正比：
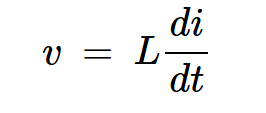方程式1我们得出结论，电感器电流的跳跃会导致电感器电压波形中的脉冲函数。请注意，我们只对电路在切换时刻（t=t0）的行为感兴趣。t=t0后的电压波形由负载网络决定，这是另一天的主题。
从方程1可以看出，从I0到0A的跳跃对应于电感器两端振幅为LI0的电压脉冲。假设整个电压尖峰出现在开关两端，我们得到图4下半部分所示的电压波形。在该曲线中，箭头终止的垂直线示出了振幅LI0的脉冲函数。
为了计算t=t0时的瞬时功率损耗，我们需要知道开关电压和电流。这两个量的乘积给出了功率损耗：
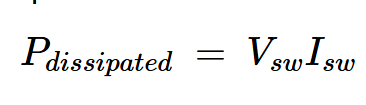方程式2从上面的讨论中，我们知道Vsw等于LI0δ（t–t0）。但是，我们仍然需要找到Isw。
由于开关电流在t=t0时从I0变为零，我们可以将此时的Isw描述为不连续点处左侧和右侧极限的平均值。因此，我们有：
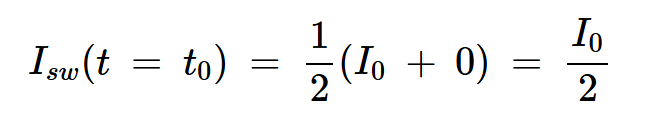方程式3将方程3代入方程2，我们得到t=t0时开关中消耗的瞬时功率：
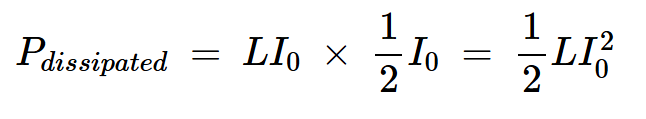方程式4将该值除以一个RF周期的持续时间（T），得出开关中消耗的平均功率：
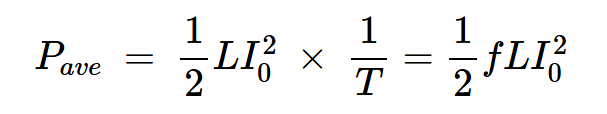方程式5其中f是开关频率。
E类零电流开关放大器
我们一直在研究的电路被称为E类零电压开关（ZVS）放大器。还有E类零电流开关（ZCS）放大器，之所以这样称呼，是因为它们在开关时刻具有零电流。当开关断开时，电流波形不会出现跳跃，而当开关接通时，电压波形会出现跳跃。如图5所示。
E类波形在开关接通时刻具有电压跳跃不连续性。
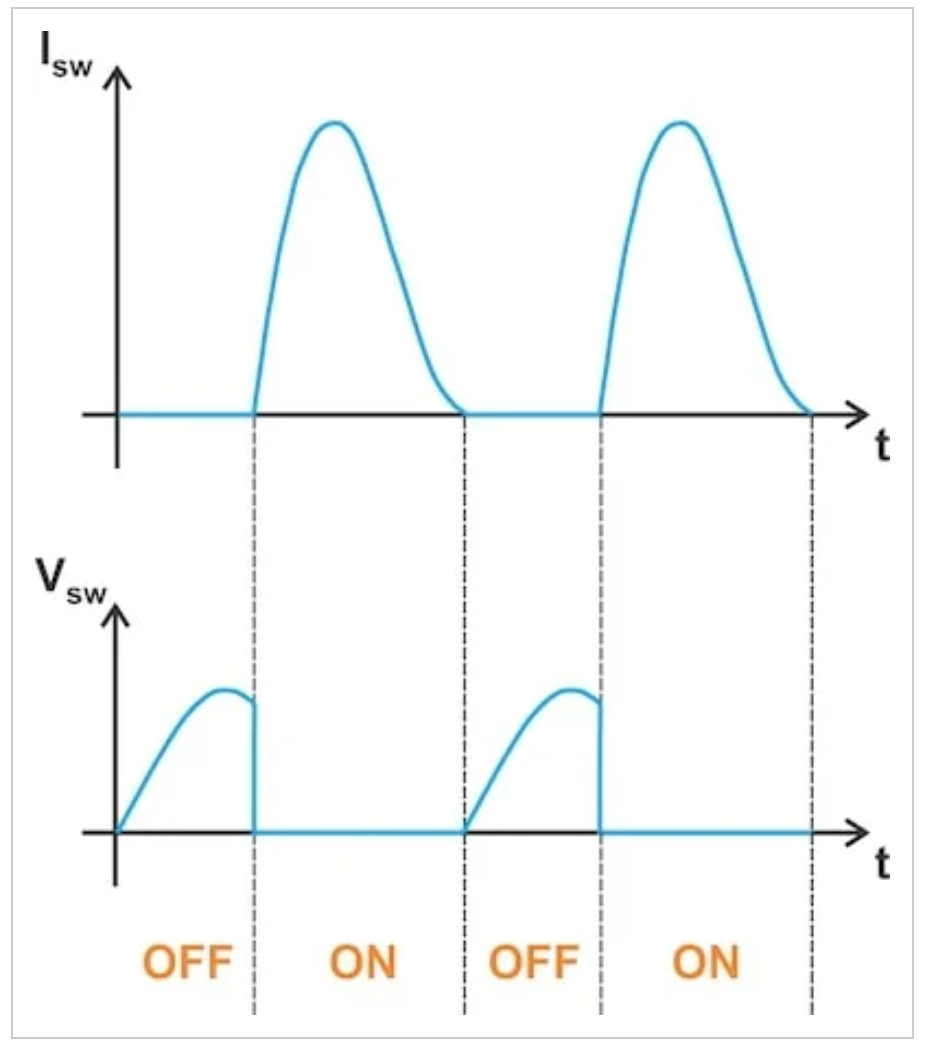图5.E类波形在开关接通时刻具有电压跳跃不连续性。图片由Steve Arar提供ZCS放大器在实际应用中通常不如ZVS放大器有吸引力，尤其是在高频下，因为它们需要一个电容可以忽略不计的开关。如果开关电容可感知，当开关接通时，电压的突然变化将导致功率损失。
总结
在下一篇文章中，我们将研究E类放大器的负载网络和瞬态响应。然后，我们将复习一些设计方程，这些方程将使我们能够轻松地为E级阶段选择组件值。请注意，我们的重点将再次放在ZVS放大器上，尽管我们可能会在本系列文章的后面回到ZCS电路。
电路
新浪科技公众号 “掌”握科技鲜闻 （微信搜索techsina或扫描左侧二维码关注）
相关新闻 